Blog WeMake

28 – Como hacer una blob animado en HTML - Parte II

Posted on Sep 16, 2021 – Updated on Sep 18, 2021 - by Franco
Cover del post

Esta es la parte II de nuestro tutorial para dibujar un blob como el de compilersforhumans.com

Si te perdiste la primera parte haz clic aquí

En esta parte veremos como dibujar un pequeño anillo 3D proyectado en una plano 2D. Veremos un poco de matemáticas, y expandiremos un poco más nuestros conocimientos de Canvas API.

Dibujando un punto 2D

Primero, dibujaremos un punto 2D en el canvas, pero esta vez usando un objeto y ya no coordenadas al azar. Vamos a tomar como referencia un plano cartesiano. Los puntos entonces no van a ser más que un conjunto de coordenadas en X, Y.

Creemos un punto, en la coordenadas (10,10)

1

const point = {x: 10, y: 10}

Como podemos ver, este punto va a tener el valor en X: 0 y en Y: 0;

Ahora a dibujarlo. Ya que un punto no tiene ni color ni radio de por si usaremos un radio de 5, y el color red. Usaremos el boilerplate code que vimos en la parte 1, y añadiremos el punto que acabamos de crear.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// 0. Setup
const canvas = document.getElementById('canvas')
const ctx = canvas.getContext('2d')
const w = canvas.width = 720 // Ancho: esto puede variarse al tamaño que quieran
const h = canvas.height = 720 // Alto: esto puede variarse al tamaño que quieran

const point = {x: 0, y: 0}

ctx.fillStyle = 'red';		// cambiamos el color de relleno a rojo
ctx.beginPath()				// 
ctx.arc(point.x,  					// coordenada en X
		  point.y, 					// coordenada en Y
			5, 					// radio del arco
			0,	 					// angulo de Inicio
			2 * Math.PI,			// angulo de fin
			true)  				// Antihorario/Horario
ctx.fill() 						// Pintamos las figuras cerradas que tenemos pendientes

Dibujando un punto 3D.

Ahora dibujaremos un punto en 3D. Primero, tenemos que dejar en claro algo, en nuestro Canvas solo podemos especificar dos coordenadas: X e Y. Para poder representar un punto en 3D necesitamos hacer lo que se conoce como una proyección. En específico usaremos una proyección proporcional, que es basicamente como perciben las cámaras de nuestros celulares las figuras 3D de nuestro mundo.

Veamos como funciona, la cámara ubicada a la izquierda asumimos que tiene un campo de visión fov de ~180 grados. Es decir que puede ver todo lo que esta en frente. El sujeto, está a la derecha, en este caso una manzana se encuentra a una distancia de la camara. Por último, el plano, se encuentra entre la cámara y el sujeto de modo que en el plano se proyecta el sujeto.

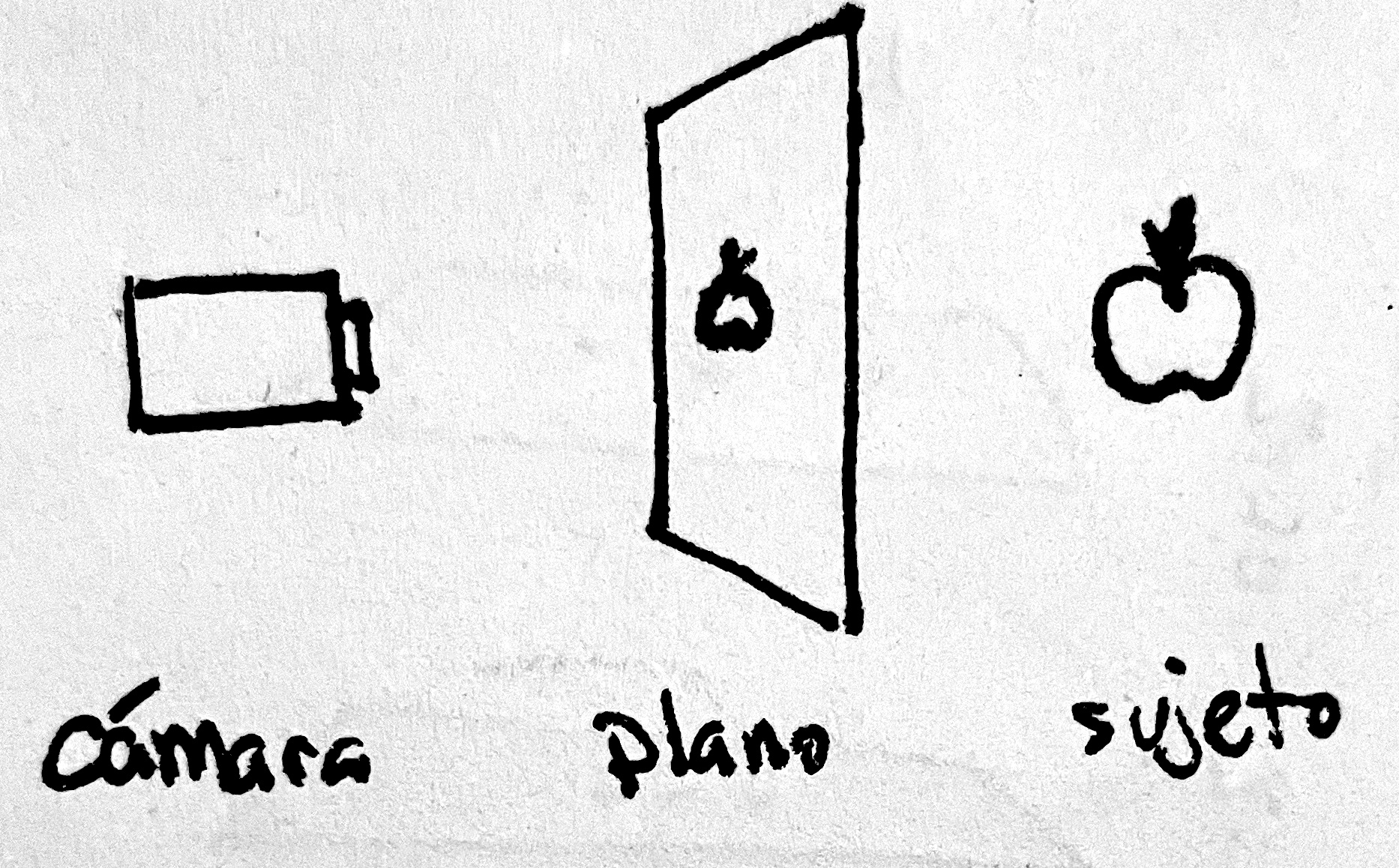
Camara, plano y sujeto

La matemática para convertir el sujeto 3D en el plano es algo trivial, solo se necesita un poco de conocimientos de trigonometría. Si no te interesa la matemática en específico puedes saltarte al parrafo que empieza con ‘Veamos la formula en javascript’.

Simplifiquemos nuestro diagrama a solo 2 puntos.

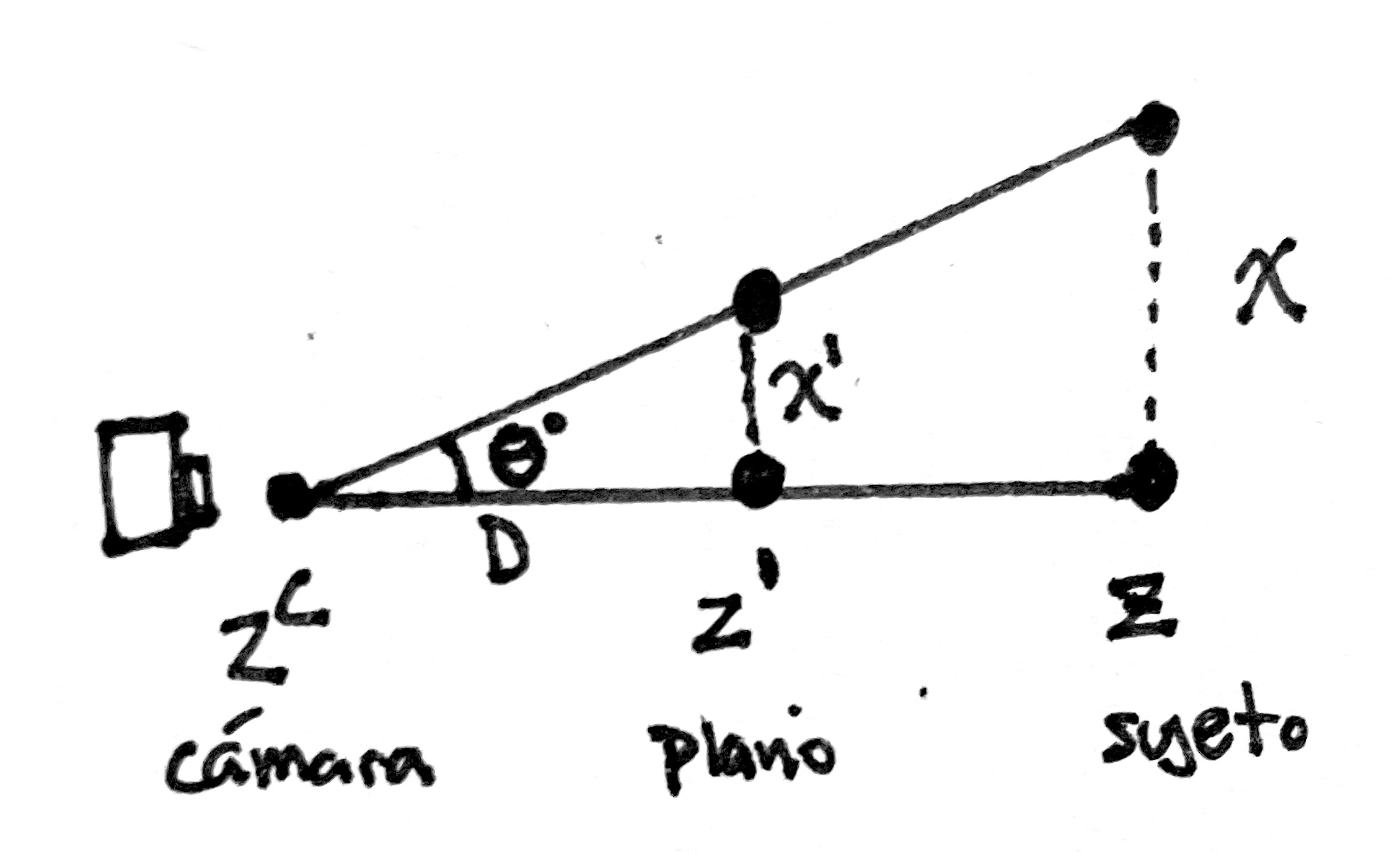
Camara, plano y sujeto simplificados

Vemos que se forma un triangulo rectángulo. Al ser un triangulo rectangulo podemos usar las identidades trigonométricas que aprendimos en el colegio: SOHCAHTOA. Es decir Seno (Opuesto sobre Hipotenusa), Coseno (Adyacente sobre Hipotenusa) y Tangente (Opuesto sobre Adyacente). Para nuestro ángulo Theta, podemos ver que el lado Adyacente es D, y el lado Opuesto es X’. Para el segundo triangulo, el más grande. Nuestro lado adyacente sería la suma de D y Z. Mientras que nuestro lado Opuesto es X.

Pásandolo a nuestras identidades trigonométricas, podemos crear la siguiente equivalencia usando la tangente.

tan(theta) = Opuesto/Adyacente
tan(theta) = X'/D					// 1
tan(theta) = X/(ZC-Z) 			// 2

Como vemos, podemos igualar 1 y 2, para formar 3.

X'/D = X/(ZC-Z) 					// 3

Usando un poco de algebra podemos despejar X'.

X' = (D*X)/(ZC-Z)					// 4

Listo, ahora tenemos la fórmula para pasar un punto (X,Z) a un punto (X’,Z’) a un plano ubicado a una distancia D de una Cámara, ubicada en ZC. A su vez, podemos pasar las coordenadas (Y, Z) usando la misma formula, a un punto en (Y’, Z’).

Veamos la fórmula en Javascript:

1
2
3

 function getProjection(distance, xy, z, z_camera) {
	return ((distance * xy) / (z_camera-z))
}

D lo escribimos como distance, XY vendria ser X o Y (dependiendo lo que le insertemos a la función), z, el punto en z y z_camera la distancia del origen a la cámara.

Ahora sí, declaremos nuestro punto 3D y dibujemoslo en el plano:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

// 0. Setup
const canvas = document.getElementById('canvas')
const ctx = canvas.getContext('2d')
const w = canvas.width = 720 // Ancho: esto puede variarse al tamaño que quieran
const h = canvas.height = 720 // Alto: esto puede variarse al tamaño que quieran

const point = {x: 10, y: 10, z: 0}

function getProjection(distance, xy, z, z_camera) {
	return ((distance * xy) / (z_camera-z))
}

const distance = 1000; 			// distancia de la camara al pano
const z_camera = 100; 			// distancia de la camara en Z

const point_in_2d = {
	x: getProjection(distance, point.x, point.z, z_camera),
	y: getProjection(distance, point.y, point.z, z_camera),
}

Primero, declaramos una distancia fija y la posición de la cámara. Luego, pasamos el punto 3D a una proyección en 2D.

Ahora a dibujamos el punto en 2d como siempre lo hemos hecho, pero empezando a contar desde la mitad del canvas (para eso el w/2 y h/2)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

//...

ctx.fillStyle = 'red';				// cambiamos el color de relleno a rojo
ctx.beginPath()						// 
ctx.arc(point_in_2d.x + w/2, 		// coordenada en X
		  point_in_2d.y + h/2, 		// coordenada en Y
			5, 							// radio del arco
			0,	 						// angulo de Inicio
			2 * Math.PI,			// angulo de fin
			true)  				// Antihorario/Horario
ctx.fill() 						// Pintamos las figuras cerradas que tenemos pendientes

Resultado:

Resultado de la proyeccion

Un pequeño puntito rojo en medio del canvas. No parece mucho, ni siquiera se nota la proyección quizás. Pero está ahi. Ahora que haremos el anillo se notará mucho más.

Esta sección fue un poco densa, pero ahora ya podemos hacer un anillo en 3D en nuestro canvas 2D.

Dibujando un anillo

Primero, veamos un pequeño sketch de lo que queremos hacer:

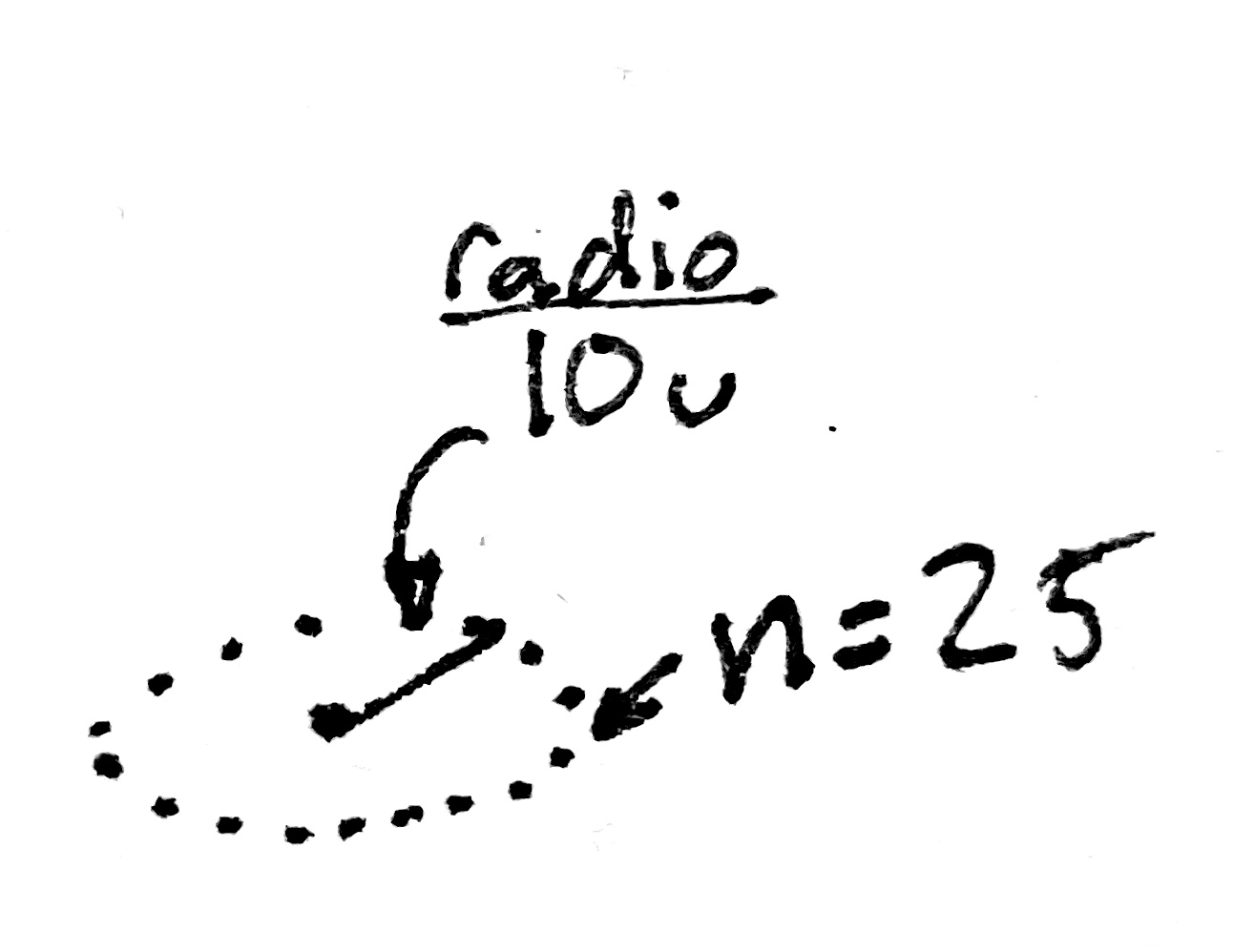
Circulo de radio 10 y 25 puntos de circunferencia

Como ven es un círculo visto de 3/4 de la horizontal. Digamos que queremos que nuestro circunferencia va a tener 25 puntos alrededor, y que tenga un radio de 10u (10 unidades).

Esta vez, para guardar los puntos vamos a usar un arreglo o “lista” de puntos.

1

const points = []

Estos puntos tendrán logicamente 3 coordenadas. Para crear los puntos haremos un pequeño for-loop (bucle) que ejecutara el código 25 veces (la cantidad de puntos que queremos). Como queremos que los puntos equidistantes vamos a dividir el largo total de la circunferencia en 25 partes iguales y poner un punto en ese lugar.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

const radius = 20; // radio del circulo
const points_in_circle = 25;
const arc_distance = (2 * Math.PI) / points_in_circle;

for(var n = 0; n < points_in_circle; n++){
	const x = Math.cos(arc_distance * n) * radius; 
	const y =  0; // nuestro circulo será paralelo al plano Y.
	const z = Math.sin(arc_distance * n) * radius;

	points.push({x, y, z}); // creamos el punto y lo insertamos en el arreglo.
}

Finalmente, tendremos que rotar en el eje X nuestros puntos para poder ver nuestra circunferencia correctamente. Esto desplazará en amount (expresado en radianes), nuestro círculo. Para conveniencia nuestra, crearemos una función que convierte grados sexagesimales a radianes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

function rotateX(point, amount){
	let y = point.y
	point.y = (y * Math.cos(amount)) + (point.z * Math.sin(amount) * -1.0)
	point.z = (y * Math.sin(amount)) + (point.z * Math.cos(amount))
	return point;
}

function radianToDegrees(angleInRadians){
	return angleInRadians * Math.PI / 180;
}

Una vez que tenemos los puntos, dibujémoslos. Para simplificar el proceso de dibujo crearemos una funcion de ayuda llamada draw_point(point, color='red', radius='5');

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

function draw_point(point, color = 'red', radius = 5){
	const distance = 1000; 			// distancia de la camara al pano
	const z_camera = 100; 			// distancia de la camara en Z

	point = rotateX(point, radianToDegrees(-10)) // Rotamos ligeramente en 10 grados

	const point_in_2d = {
		x: getProjection(distance, point.x, point.z, z_camera),
		y: getProjection(distance, point.y, point.z, z_camera),
	}

	ctx.fillStyle = color;				// cambiamos el color de relleno a rojo
	ctx.beginPath()						// 
	ctx.arc(point_in_2d.x + w/2, 		// coordenada en X
			point_in_2d.y + h/2, 		// coordenada en Y
			radius, 							// radio del arco
			0,	 								// angulo de Inicio
			2 * Math.PI,					// angulo de fin
			true)  							// Antihorario/Horario
	ctx.fill() 								// Pintamos las figuras cerradas que tenemos pendientes
}

Por último, veremos como usaremos esta función:

1
2
3

for(const point in points){
	draw_point(point);
}

Integrando todo, obtenemos lo siguiente:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

<html lang="en">
	<head>
		<meta charset="UTF-8">
  		<meta http-equiv="X-UA-Compatible" content="IE=edge">
  		<meta name="viewport" content="width=device-width, initial-scale=1.0">
  		<title>Sphere</title>
		<style>
			/* ESTILOS */
		</style>
	</head>
	<body>
		<h1> Sphere.  </h1>
		<h2> <span id="x"> X </span> WeMake.  </h2>
		<canvas id="canvas"></canvas>
	<script>
// 0. Setup
const canvas = document.getElementById('canvas')
const ctx = canvas.getContext('2d')
const w = canvas.width = 720 // Ancho: esto puede variarse al tamaño que quieran
const h = canvas.height = 720 // Alto: esto puede variarse al tamaño que quieran

function getProjection(distance, xy, z, z_camera) {
	return ((distance * xy) / (z_camera- z))
}

const points = [] 	// lista o arreglo de puntos
const radius = 20; 	// radio del circulo
const points_in_circle = 100;
const arc_distance = (2 * Math.PI) / points_in_circle;

for(var n = 0; n < points_in_circle; n++){
	const x = Math.cos(arc_distance * n) * radius; 
	const y = 0; // nuestro circulo será paralelo al plano Y.
	const z = Math.sin(arc_distance * n) * radius;

	points.push({x, y, z}); // creamos el punto y lo insertamos en el arreglo.
}

function rotateX(point, amount){
	let y = point.y
	point.y = (y * Math.cos(amount)) + (point.z * Math.sin(amount) * -1.0)
	point.z = (y * Math.sin(amount)) + (point.z * Math.cos(amount))
	return point;
}

function radianToDegrees(angleInRadians){
	return angleInRadians * Math.PI / 180;
}

function draw_point(point, color = 'red', radius = 5){
	const distance = 1000; 			// distancia de la camara al plano
	const z_camera = 100; 			// distancia de la camara en Z

	point = rotateX(point, radianToDegrees(-10)) // Rotamos ligeramente en 10 deg

	const point_in_2d = {
		x: getProjection(distance, point.x, point.z, z_camera),
		y: getProjection(distance, point.y, point.z, z_camera),
	}

	ctx.fillStyle = color;				// cambiamos el color de relleno a rojo
	ctx.beginPath()						// 
	ctx.arc(point_in_2d.x + w/2, 		// coordenada en X
			point_in_2d.y + h/2, 		// coordenada en Y
			radius, 							// radio del arco
			0,	 								// angulo de Inicio
			2 * Math.PI,					// angulo de fin
			true)  							// Antihorario/Horario
	ctx.fill() 								// Pintamos las figuras cerradas que tenemos pendientes
}

		for(const point of points){
			draw_point(point);
		}
	</script>
	</body>
</html>

Y el resultado, una bella circunferencia ligeramente rotada: Los puntos más cercanos se ven más juntos dada su proximidad. Y los puntos más alejados se separan ligeramente debido a que estan más lejos de la cámara.

Resultado

Por ultimo cambiemos la variable points_in_circle a un valor mayor, como 100 y veamos el resultado:

Resultado

🥳 Excelente, podemos ver ahora claramente nuestra circunferencia.

Este post ha sido algo extenso, pero espero que hayan aprendido varias cosas, solo les recomiendo que jueguen con las variables, aprendan que hace cada una de ellas, entiendan el código, y si pueden las matemáticas que hemos usado.

En la siguiente parte (Parte III) veremos como construir la esfera completa basándonos en este circunferencia, y como rotarla.